GitHub repository: https://github.com/Noavem/Hack-assembler
Some time ago, I built an assembler for the Hack Assembly language, as described in The Elements of Computing Systems. During this endeavor, I discovered that the C standard library does not provide a hash table implementation, so I decided to implement my own.
As you might guess from its name, a hash table uses hashing to store and retrieve values efficiently. There are many hashing algorithms out there; one of which is Pearson hashing. In this post, I’ll explain how I used the Pearson hashing algorithm to implement a hash table, and how that table served my Hack assembler.
The Hack Assembly language supports a relatively small set of instructions, each of which corresponds to a unique 16-bit sequence. This sequence is the machine code that is read by the CPU. Below are some examples of assembly instructions and their corresponding machine code:
| Assembly instruction | Machine code |
|---|---|
| @7 | 0000000000000111 |
| DM=M+1 | 1111110111011000 |
| A=D | 1110001100100000 |
In this regard, the Hack Assembly language is extremely simple, as each instruction can be mapped directly onto a 16-bit machine code sequence. Compared to behemoths like x86 assembly, this is child’s play (though assemblers for those languages weren’t exactly created in a few hours either).
Before diving into Pearson hashing specifically, let’s talk about hashing in general and why it’s incredibly useful when building an assembler (or really, any kind of translator). In digital computing, hashing is the process of transforming data of arbitrary size into a fixed-size bit sequence. This might seem unremarkable at first, but let’s walk through an example to show its usefulness.
Say we want to translate the Hack assembly instruction D=A into machine code. According to the Hack Machine Language Specification, an assignment like this is converted into a binary instruction that follows this format:
// `dest` is commonly known is the lvalue, `comp` as the rvalue
111{7-bit comp sequence}{3-bit dest sequence}000In the case of D=A, the mnemonic D corresponds to 010, and A corresponds to 0110000. That means the Hack instruction D=A is translated to the 16-bit machine code 1110110000010000.
So, the assembler needs a way to store and efficiently retrieve the bit sequence associated with each mnemonic. One simple approach is to use an array of key-value pairs:
[("D+1", "001111"), ("A", "110000"), ...]Then, whenever a mnemonic appears in the assembly code, the assembler searches the array to find the corresponding bit sequence. This kind of linear search works well enough for a small number of mnemonics, but it becomes increasingly inefficient as the set grows. In the worst case, you have to scan the entire array just to find one match.
This is where hashing comes in. Instead of linearly searching through an entire array, we can hash the mnemonic (e.g. D, A or M+1) to produce a fixed-size number. That number becomes the index where we store (or look up) the corresponding bit sequence in an array or table. This results in constant-time retrieval on average.
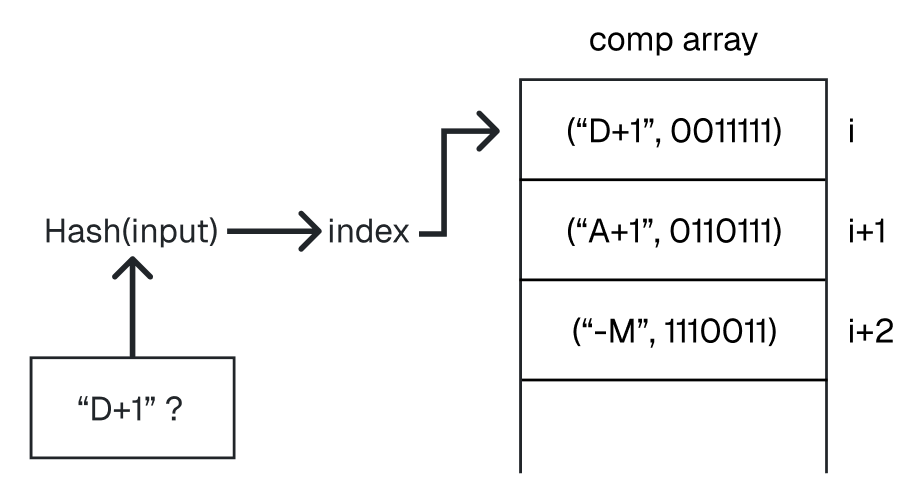
To make this work, we use a hash table instead of a plain array. Rather than storing pairs in a list and searching through them one by one, we use a hash function that takes a string (like "D+1") and spits out a number. That number tells us exactly where to store and retrieve the corresponding bit sequence; at least, in theory (we’ll cover collisions later on).
The process of storing and retrieving a value might look like this:
mnemonic_map = [None] * MAP_SIZE
/* We'll cover collisions later on */
def store(mnemonic, bit_sequence):
index = hash(mnemonic)
mnemonic_map[resolve_collision(index, mnemonic)] = bit_sequence
def lookup(mnemonic):
index = hash(mnemonic)
return mnemonic_map[resolve_collision(index, mnemonic)]
/* Storing (mnemonic, bit-sequence) pairs */
store("D+1", "001111")
store("A", "110000")
/* Translating a mnemonic to its bit-sequence */
lookup("D+1") // -> "001111"
So far, so good. But how does the hashing actually work?
There are countless hashing algorithms out there, but in this post, I’ll describe Pearson hashing. It’s simple to implement and supported by basic instruction sets present on virtually every microprocessor.
Pearson hashing was introduced by Peter K. Pearson in his article Fast Hashing of Variable-Length Text Strings. Below is a possible implementation in C:
uint8_t pearson_hashing(const char *input) {
uint8_t hash = 0;
for (size_t i = 0; i < strlen(input); i++) {
hash = T[hash ^ (uint8_t)input[i]];
}
return hash;
}It’s important to note that, as with any good hashing function, even a tiny change in the input should produce a wildly different output. This property (known as the avalanche effect) is essential for minimizing collisions and ensuring a good distribution of hash values. The implementation of this algorithm isn’t all that special, but the observant reader might have noticed a mysterious array called T. This array represents some permutation of the integers 0 through 255 (internally stored as 8-bit sequences).
This permutation table plays a crucial role in the behavior and efficiency of the Pearson hashing algorithm. It should be a randomized ordering of the set {0, 1, 2, ..., 255}. A poor choice of permutation can severely impact the efficiency of the hash table. For example, using the identity permutation **(**where T[x] = x) is especially bad as it fails to separate anagrams. Using the identity permutation simplifies hash to:
/* Identity permutation, thus T[x] = x */
hash = hash ^ (uint8_t)input[i]Now let’s consider anagrams $S_a$ and $S_b$ of length $n$. Assuming we use the identity permutation, the hashes of these anagrams would be:
$S_a = c_{a_1} ⊕ c_{a_2} ⊕ … ⊕ c_{a_n}$
$S_b = c_{b_1} ⊕ c_{b_2} ⊕ … ⊕ c_{b_n}$.
And due to XOR’s commutative property, these outputs are equal. Thus, using the identity permutation for Pearson Hashing causes anagrams to always result in the same hash value (which could heavily increase the amount of collisions).
A good permutation should be random enough to promote the avalanche effect (such that even the slightest change in input causes a big and unpredictable change in output). I’ll explore the avalanche effect more thoroughly in a future post.
Fortunately, Peter K. Pearson provided a permutation with empirically satisfying results in his article:
uint8_t T[256] = {
1, 87, 49, 12, 176, 178, 102, 166, 121, 193, 6, 84, 249, 230, 44, 163,
14, 197, 213, 181, 161, 85, 218, 80, 64, 239, 24, 226, 236, 142, 38, 200,
110, 177, 104, 103, 141, 253, 255, 50, 77, 101, 81, 18, 45, 96, 31, 222,
25, 107, 190, 70, 86, 237, 240, 34, 72, 242, 20, 214, 244, 227, 149, 235,
97, 234, 57, 22, 60, 250, 82, 175, 208, 5, 127, 199, 111, 62, 135, 248,
174, 169, 211, 58, 66, 154, 106, 195, 245, 171, 17, 187, 182, 179, 0, 243,
132, 56, 148, 75, 128, 133, 158, 100, 130, 126, 91, 13, 153, 246, 216, 219,
119, 68, 223, 78, 83, 88, 201, 99, 122, 11, 92, 32, 136, 114, 52, 10,
138, 30, 48, 183, 156, 35, 61, 26, 143, 74, 251, 94, 129, 162, 63, 152,
170, 7, 115, 167, 241, 206, 3, 150, 55, 59, 151, 220, 90, 53, 23, 131,
125, 173, 15, 238, 79, 95, 89, 16, 105, 137, 225, 224, 217, 160, 37, 123,
118, 73, 2, 157, 46, 116, 9, 145, 134, 228, 207, 212, 202, 215, 69, 229,
27, 188, 67, 124, 168, 252, 42, 4, 29, 108, 21, 247, 19, 205, 39, 203,
233, 40, 186, 147, 198, 192, 155, 33, 164, 191, 98, 204, 165, 180, 117, 76,
140, 36, 210, 172, 41, 54, 159, 8, 185, 232, 113, 196, 231, 47, 146, 120,
51, 65, 28, 144, 254, 221, 93, 189, 194, 139, 112, 43, 71, 109, 184, 209
};Now that we understand the 8-bit version of this algorithm, let’s look at how we can expand it to return a full 16-bit hash (allowing us to store more mnemonics if necessary):
uint16_t pearson_hashing(const char *input) {
uint8_t hash1 = 0;
uint8_t hash2 = 0;
for (size_t i = 0; i < strlen(input); i++) {
hash1 = T[hash1 ^ (uint8_t)input[i]];
}
hash2 = T[hash1 ^ ((uint8_t)input[0]+1)];
for (size_t i = 1; i < strlen(input); i++) {
hash2 = T[hash2 ^ (uint8_t)input[i]];
}
uint16_t hash = ((uint16_t)hash1 << 8) | hash2;
return hash;
}This expansion is mostly self-explanatory, with one exception: the initialization of hash2 using this line:
hash2 = T[hash1 ^ ((uint8_t)input[0] + 1)];The purpose of this expression is to ensure that hash2 doesn’t simply mirror hash1. If we reused the same initial value for both, we’d produce identical outputs (effectively collapsing our supposedly 16-bit hash back down to just 8 bits). This would heavily increase the chance of collisions, defeating the entire purpose of the extension. By tweaking the starting value of hash2, we diversify the second pass and make better use of the 16-bit output space.
Let’s circle back to our assembler.
As mentioned earlier, we need a way to store and retrieve all mnemonics and their corresponding bit sequences. To do this, we first create an array large enough to hold all the entries (and preferably quite a bit bigger, as it reduces the probability of collisions).
To store a mnemonic and its corresponding bit sequence, we place the pair at index:
hash(mnemonic) % array_sizeIf there’s already another entry at that index (a collision), we simply increment the index, probing linearly, until we find an empty slot. Likewise, to look up a bit sequence for a given mnemonic, we start at the index computed by hash(mnemonic) % array_size and keep checking subsequent slots until we find the matching mnemonic.
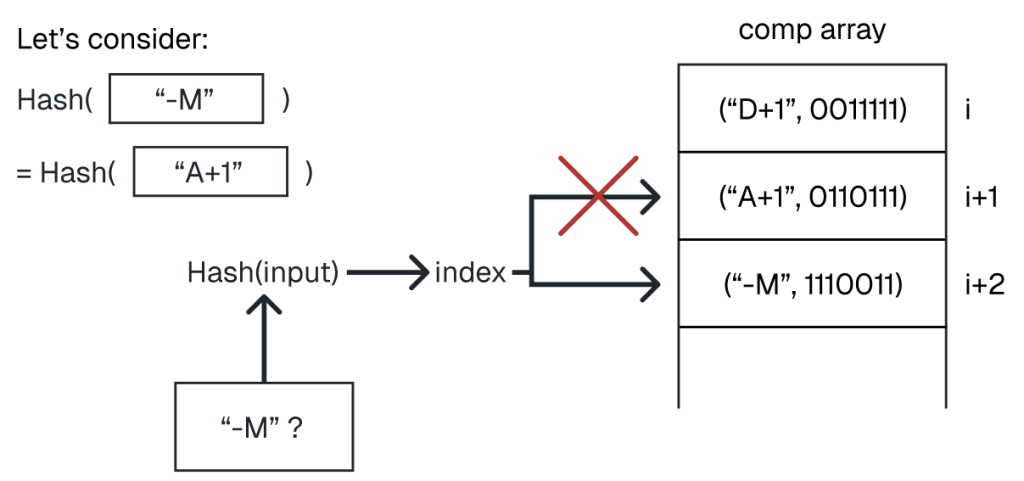
The Pearson hashing algorithm is elegantly simple and quite usable in real-world applications. However, its primary drawback is the need to store a full 256-byte permutation table. On most systems, this is trivial; but in constrained embedded environments, that memory footprint can be a concern.
One alternative is to generate the permutation dynamically using a function instead of a lookup table. But this typically increases the amount of collisions and reduces the hash’s quality. It’s a classic case of space–time tradeoff: fewer bytes, more collisions; more bytes, faster retrieval.
